library(readr)
library(dplyr)
library(ppcor) # Para correlaciones parciales
library(ggplot2)
library(ggrepel)
library(MASS) # Para studres()
library(lmtest) # Para bptest() y resettest()
library(car) # Para vif() e influencePlot()
library(RColorBrewer) # Para paletas de colores11 Proyecto 2
12 Introducción
Este documento presenta un análisis de regresión lineal múltiple para modelar y predecir la cantidad de goles anotados por futbolistas. El análisis abarca desde la exploración de correlaciones entre las variables predictoras y la variable de respuesta, hasta el ajuste de un modelo completo, su validación rigurosa mediante pruebas de supuestos y un diagnóstico detallado para identificar observaciones influyentes.
12.0.1 Librerías Requeridas
Se cargan únicamente los paquetes necesarios para la ejecución de este análisis.
12.0.2 Carga y Exploración de Datos
sapo2 <- read.csv("DataBase_Proyecto2.csv", comment.char = "#")
# View(sapo2)13 1. Análisis de Correlación
Se explora la relación lineal entre la variable de respuesta (Goles) y las variables predictoras. Se calculan tres tipos de correlaciones:
- Pearson (\(r\)): Mide la relación lineal.
- Kendall (\(\tau\)): Mide la asociación monotónica (basada en rangos).
- Parcial: Mide la relación entre dos variables controlando el efecto de las demás.
# Correlaciones (incluyendo variables de equipo)
round(cor(sapo2[, c(12, 8, 9, 10, 11)]), digits = 4) Goles Partidos Tiros Tiempo xGoals
Goles 1.0000 0.7360 0.8800 0.7473 0.9331
Partidos 0.7360 1.0000 0.8643 0.9959 0.7510
Tiros 0.8800 0.8643 1.0000 0.8738 0.9104
Tiempo 0.7473 0.9959 0.8738 1.0000 0.7639
xGoals 0.9331 0.7510 0.9104 0.7639 1.0000round(pcor(sapo2[, c(12, 8, 9, 10, 11)])$estimate, digits = 4) Goles Partidos Tiros Tiempo xGoals
Goles 1.0000 0.0106 0.1440 -0.0076 0.6662
Partidos 0.0106 1.0000 -0.0080 0.9835 -0.0827
Tiros 0.1440 -0.0080 1.0000 0.1270 0.4719
Tiempo -0.0076 0.9835 0.1270 1.0000 0.0583
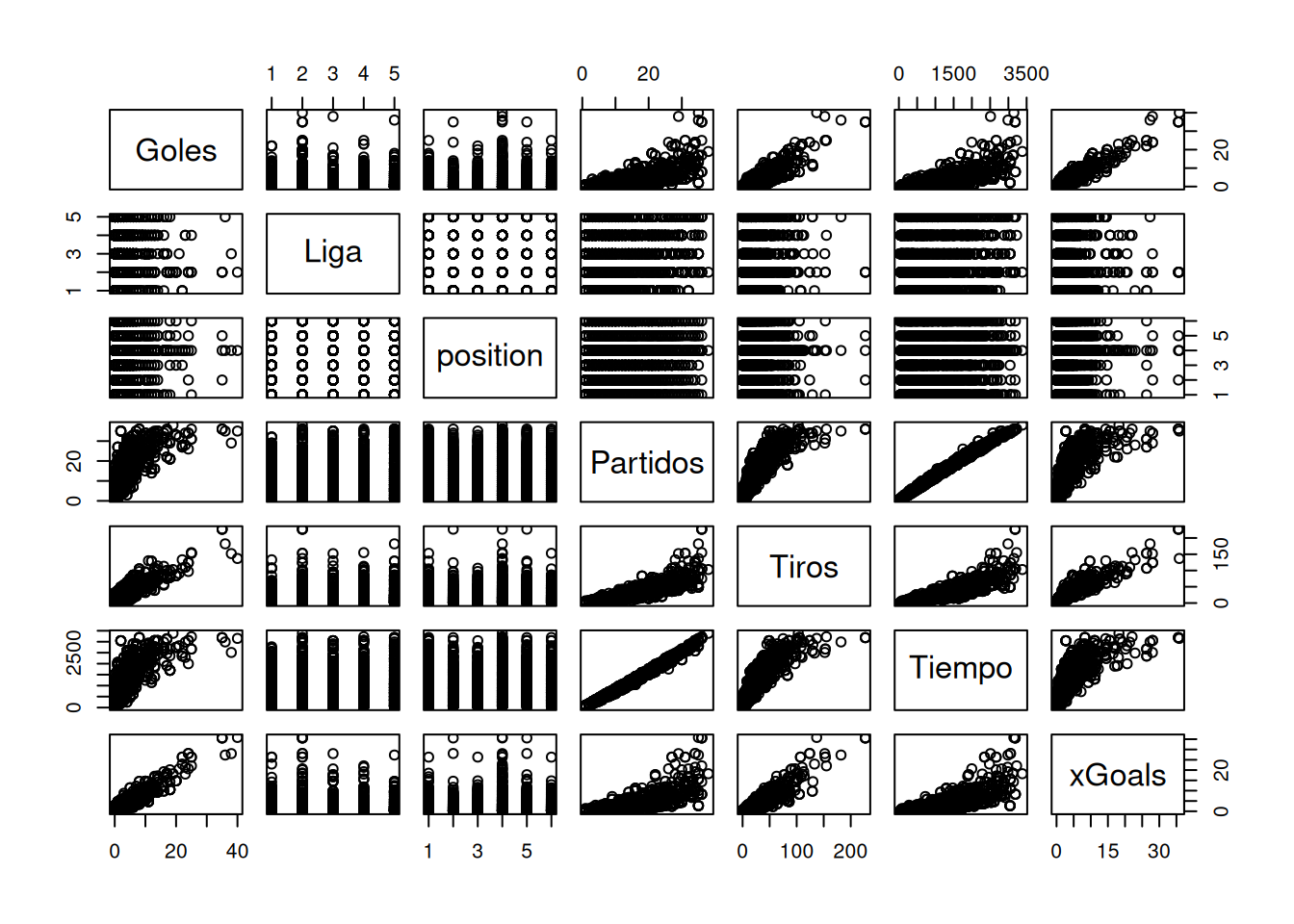
xGoals 0.6662 -0.0827 0.4719 0.0583 1.0000plot(sapo2[, c(12, 4, 6, 8, 9, 10, 11)])14 2. Análisis Descriptivo por Grupos
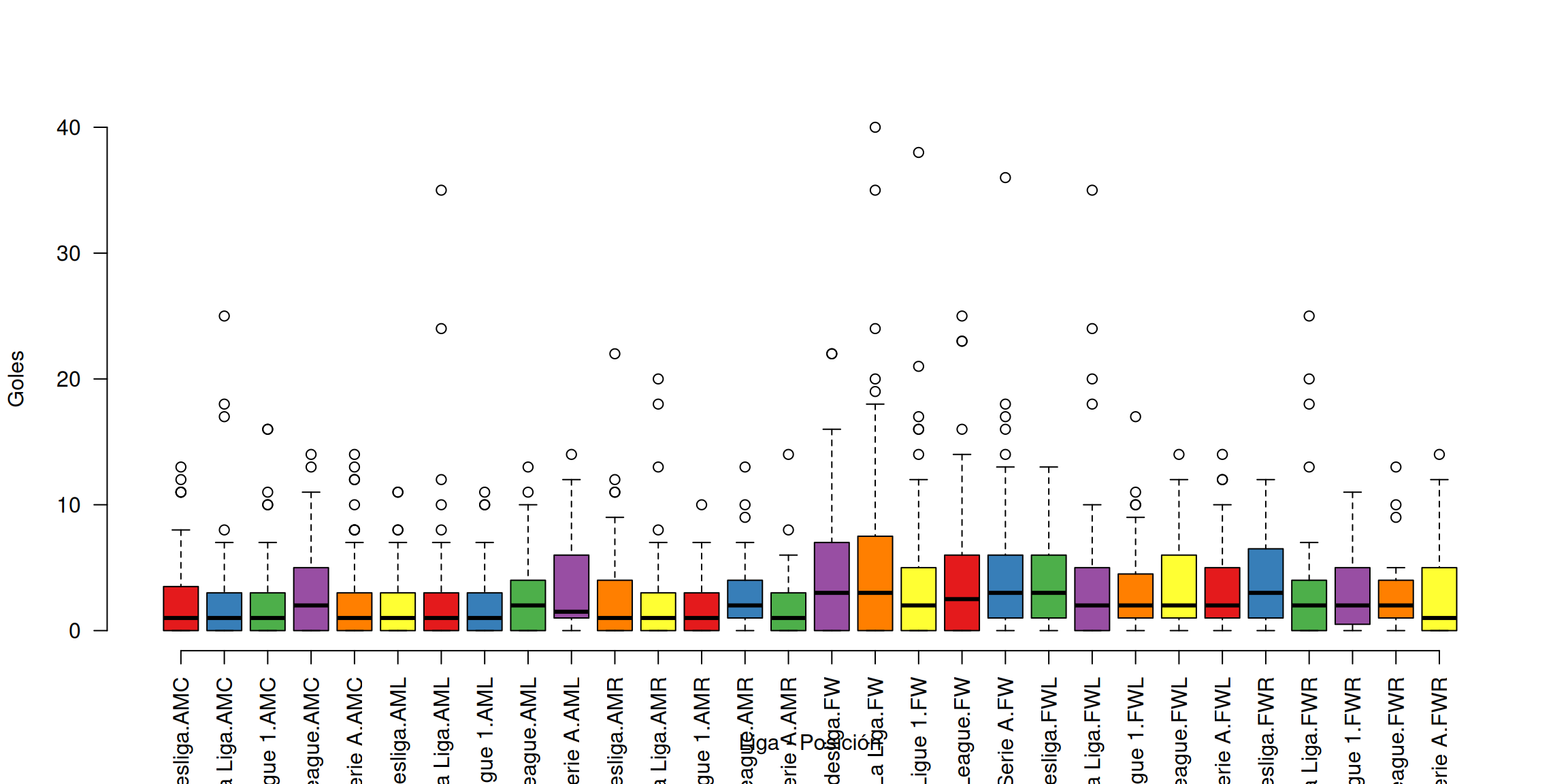
Se visualiza cómo varía la cantidad de goles según la liga y la posición del jugador mediante boxplots.
15 3. Modelo de Regresión Lineal Múltiple
Se ajusta un modelo para predecir los goles en función de la liga, la posición, los tiros, el tiempo jugado y los goles esperados (xGoals). El modelo es de la forma: \[ \text{Goles}_i = \beta_0 + \beta_1 \text{Liga}_i + \dots + \beta_k \text{xGoals}_i + \epsilon_i \]
modelo <- lm(Goles ~ 1 + Liga + position + Tiros + Tiempo + xGoals, data = sapo2)
summary(modelo)
Call:
lm(formula = Goles ~ 1 + Liga + position + Tiros + Tiempo + xGoals,
data = sapo2)
Residuals:
Min 1Q Median 3Q Max
-6.2130 -0.7382 -0.0401 0.4843 10.2326
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.265e-01 1.128e-01 -1.122 0.262
LigaLa Liga -8.407e-02 1.106e-01 -0.760 0.447
LigaLigue 1 -7.349e-03 1.093e-01 -0.067 0.946
LigaPremier League 3.876e-02 1.125e-01 0.345 0.730
LigaSerie A -9.308e-02 1.196e-01 -0.778 0.437
positionAML -4.310e-02 1.154e-01 -0.373 0.709
positionAMR -5.470e-02 1.157e-01 -0.473 0.636
positionFW -1.084e-01 1.052e-01 -1.031 0.303
positionFWL -1.019e-02 1.313e-01 -0.078 0.938
positionFWR -2.326e-03 1.279e-01 -0.018 0.985
Tiros 2.775e-02 4.440e-03 6.250 5.04e-10 ***
Tiempo 5.817e-05 9.320e-05 0.624 0.533
xGoals 8.447e-01 2.201e-02 38.375 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.521 on 1931 degrees of freedom
Multiple R-squared: 0.8763, Adjusted R-squared: 0.8755
F-statistic: 1140 on 12 and 1931 DF, p-value: < 2.2e-16# Tabla de coeficientes
round(as.data.frame(modelo$coefficients), digits = 7) modelo$coefficients
(Intercept) -0.1265409
LigaLa Liga -0.0840666
LigaLigue 1 -0.0073493
LigaPremier League 0.0387622
LigaSerie A -0.0930819
positionAML -0.0430968
positionAMR -0.0546982
positionFW -0.1084056
positionFWL -0.0101908
positionFWR -0.0023258
Tiros 0.0277460
Tiempo 0.0000582
xGoals 0.844726716 4. Validación de Supuestos del Modelo
Se realizan pruebas formales y diagnósticos gráficos para verificar los supuestos del modelo de regresión lineal.
# Se extraen los residuales estudentizados
stud_res <- studres(modelo)16.1 4.1. Linealidad (Test RESET)
La prueba RESET (Regression Equation Specification Error Test) evalúa si la forma funcional del modelo es correcta (linealidad). - \(H_0\): La especificación del modelo es correcta (la relación es lineal).
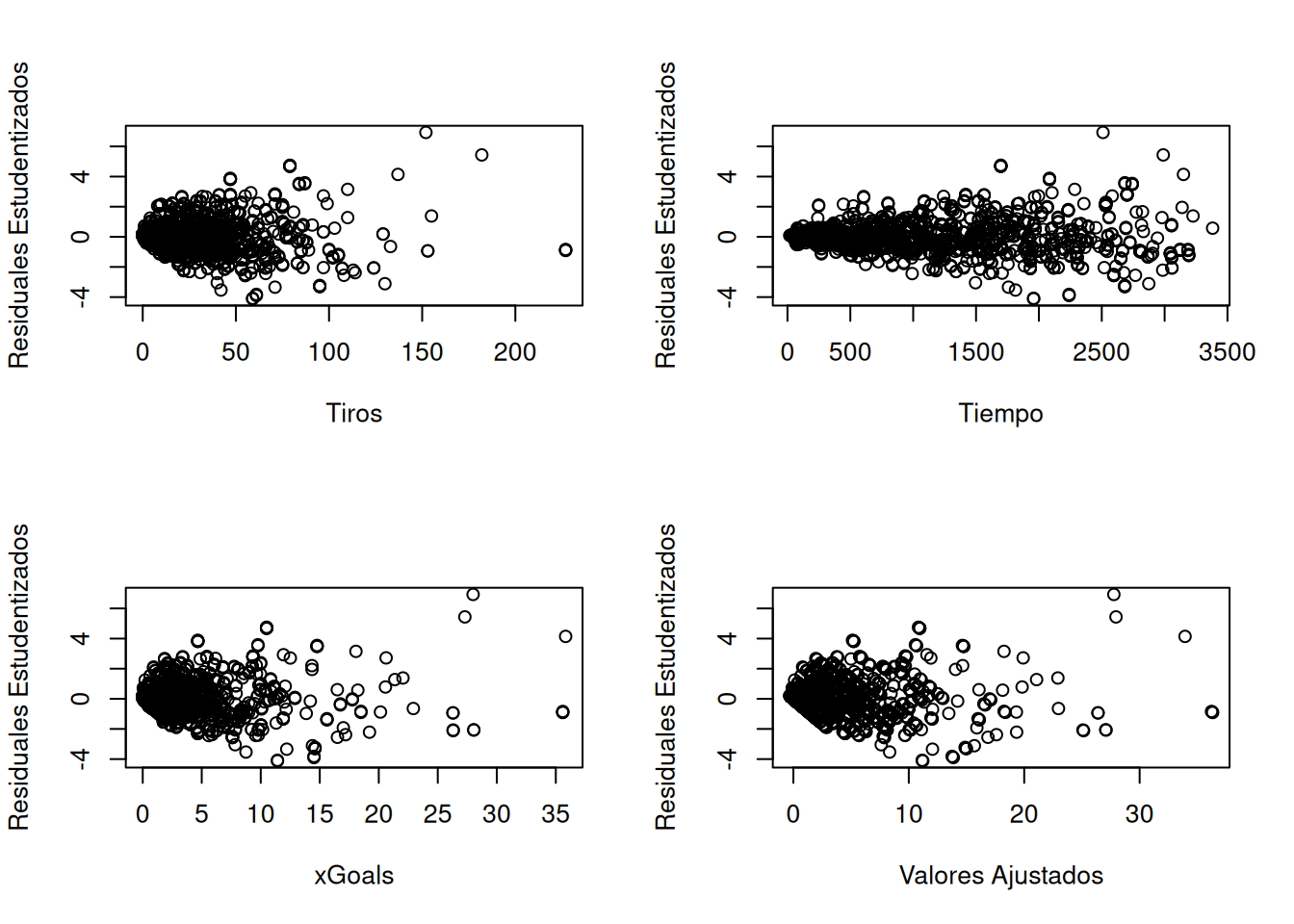
# Gráficos de residuales vs. predictores y vs. valores ajustados
par(mfrow=c(2,2))
plot(sapo2$Tiros, stud_res, xlab = "Tiros", ylab = "Residuales Estudentizados")
plot(sapo2$Tiempo, stud_res, xlab = "Tiempo", ylab = "Residuales Estudentizados")
plot(sapo2$xGoals, stud_res, xlab = "xGoals", ylab = "Residuales Estudentizados")
plot(fitted(modelo), stud_res, xlab = "Valores Ajustados", ylab = "Residuales Estudentizados")par(mfrow=c(1,1))
# Test RESET
resettest(modelo, power = 2:5, type = "fitted")
RESET test
data: modelo
RESET = 4.7507, df1 = 4, df2 = 1927, p-value = 0.0008151Conclusión: El p-valor pequeño sugiere rechazar \(H_0\), indicando una posible falta de linealidad.
16.2 4.2. Media Cero y Normalidad de los Residuales
# Media de los residuales (debe ser cercana a cero por construcción)
mean(modelo$residuals)[1] 1.267362e-17# Prueba t para H0: media de los residuos = 0
t.test(modelo$residuals, mu = 0)
One Sample t-test
data: modelo$residuals
t = 3.6841e-16, df = 1943, p-value = 1
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.067466 0.067466
sample estimates:
mean of x
1.267362e-17 # Prueba de Shapiro-Wilk para H0: los residuales siguen una distribución normal
shapiro.test(stud_res)
Shapiro-Wilk normality test
data: stud_res
W = 0.92308, p-value < 2.2e-16Conclusión: Se cumple el supuesto de media cero. Sin embargo, el p-valor de la prueba de Shapiro-Wilk es muy pequeño, rechazando el supuesto de normalidad en los residuales.
16.3 4.3. Homocedasticidad (Varianza Constante)
Se evalúa si la varianza de los errores es constante. - \(H_0\): Hay homocedasticidad (varianza constante).
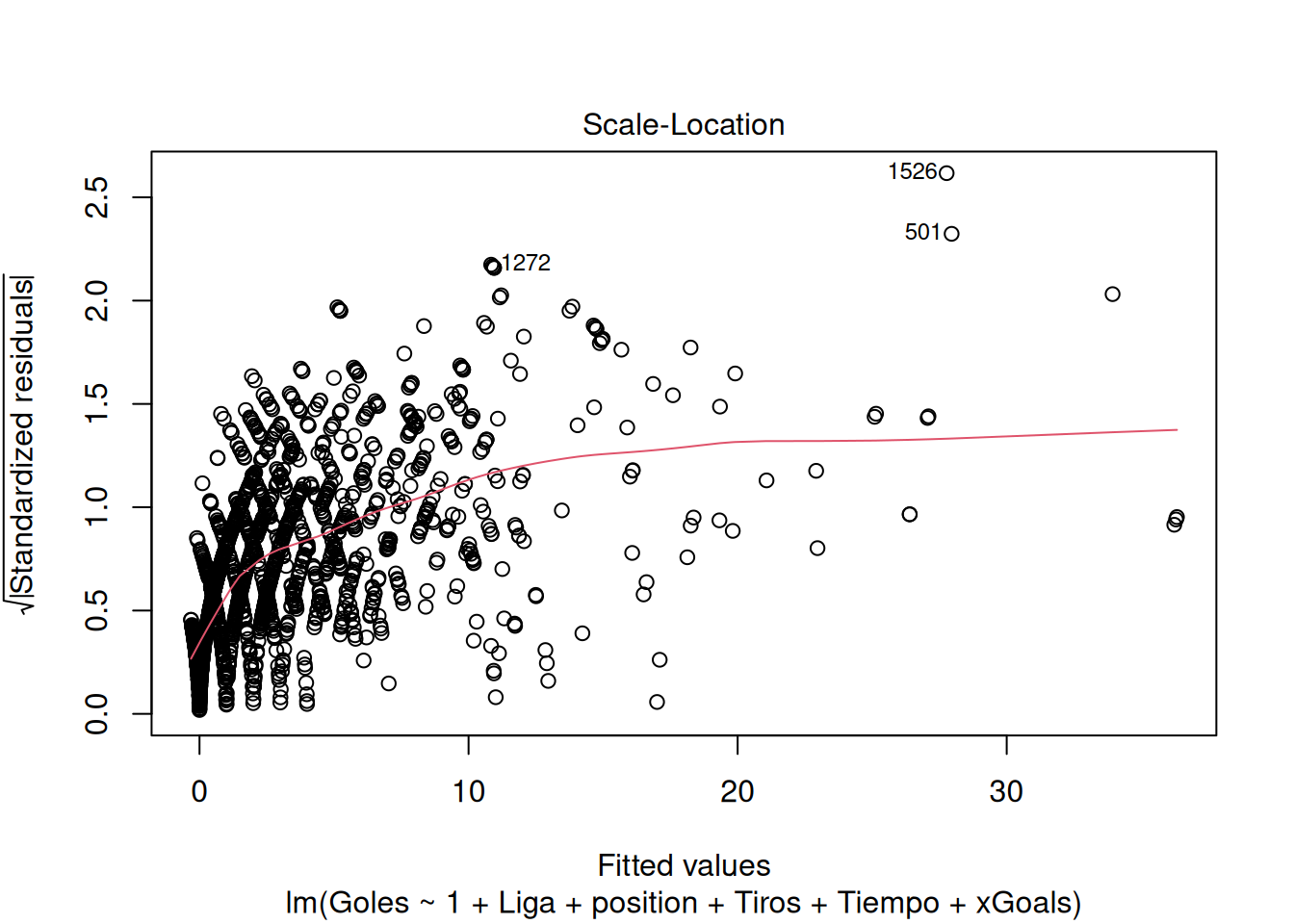
# Gráfico de Scale-Location
plot(modelo, which = 3)# Test de Breusch-Pagan
bptest(modelo)
studentized Breusch-Pagan test
data: modelo
BP = 449.13, df = 12, p-value < 2.2e-16Conclusión: El p-valor pequeño rechaza \(H_0\), indicando la presencia de heterocedasticidad (varianza no constante).
16.4 4.4. Multicolinealidad
Se evalúa la correlación entre las variables predictoras. El Factor de Inflación de la Varianza (VIF) mide cuánto aumenta la varianza de un coeficiente debido a la colinealidad. - Regla general: VIF > 5 o 10 indica un problema de multicolinealidad.
car::vif(modelo) GVIF Df GVIF^(1/(2*Df))
Liga 1.093472 4 1.011232
position 1.146205 5 1.013739
Tiros 10.767639 1 3.281408
Tiempo 4.362029 1 2.088547
xGoals 6.412345 1 2.532261Conclusión: Todos los VIF son bajos, lo que sugiere que no hay problemas graves de multicolinealidad.
17 5. Análisis de Diagnóstico: Puntos Influyentes
Se identifican observaciones que pueden tener un efecto desproporcionado en el ajuste del modelo.
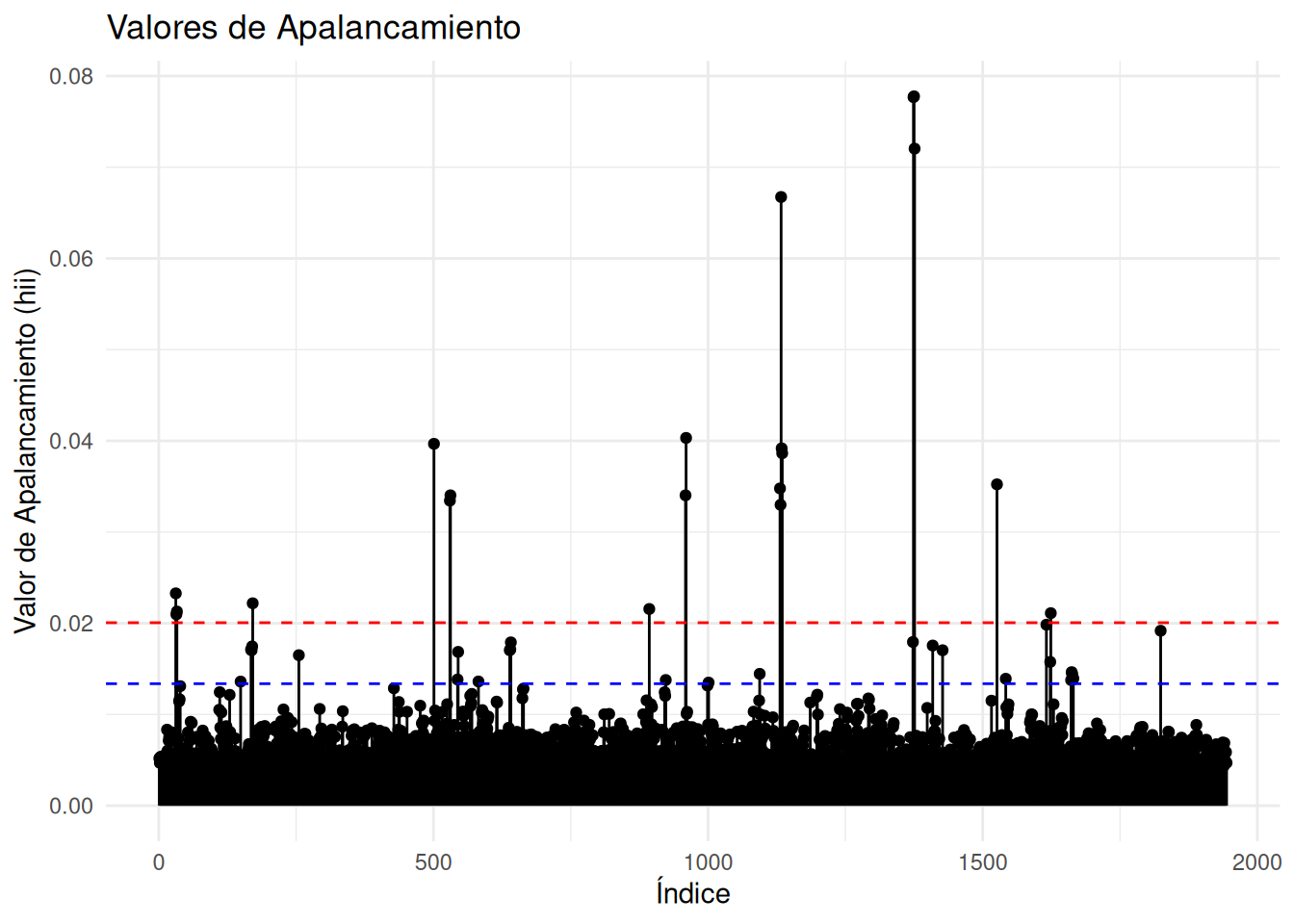
17.1 5.1. Observaciones con Alta Palanca (Leverage)
Puntos con valores atípicos en los predictores. Un punto tiene alta palanca si su valor “hat” \(h_{ii} > 2p/n\) o \(3p/n\).
X <- model.matrix(modelo)
H <- X %*% solve(t(X) %*% X) %*% t(X)
p <- sum(hatvalues(modelo))
n <- nrow(sapo2)
h_ii <- as.data.frame(cbind(index = 1:n, hat_value = diag(H)))
ggplot(h_ii, aes(x = index, y = hat_value, label = index)) +
geom_segment(aes(xend = index, yend = 0)) +
geom_point() +
geom_hline(yintercept = 3 * p / n, color = "red", linetype = "dashed") +
geom_hline(yintercept = 2 * p / n, color = "blue", linetype = "dashed") +
labs(x = "Índice", y = "Valor de Apalancamiento (hii)", title = "Valores de Apalancamiento") +
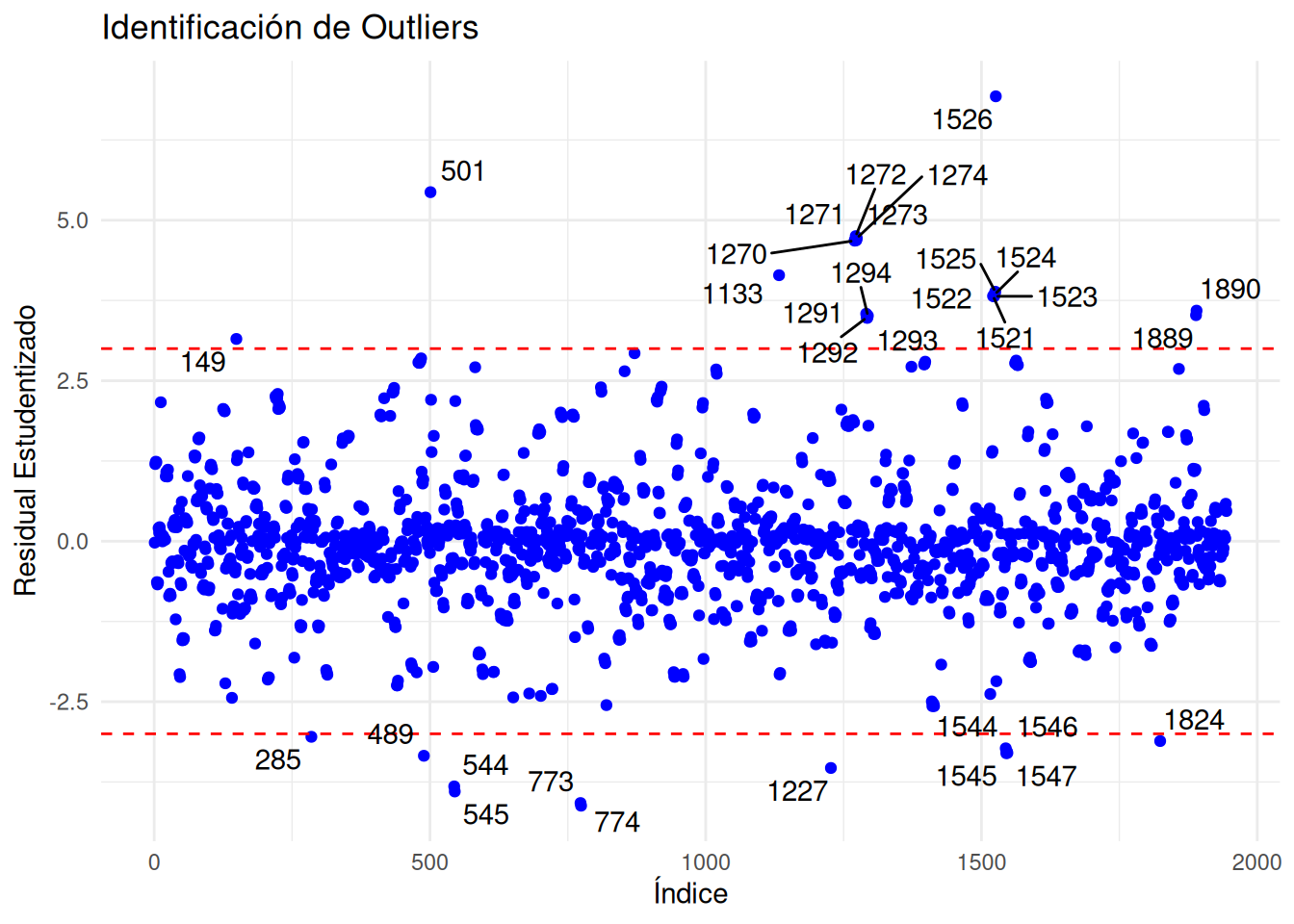
theme_minimal()17.2 5.2. Observaciones Atípicas (Outliers)
Puntos con un gran error de predicción. Se identifican usando los residuales estudentizados. Un punto es atípico si \(|r_{i, stud}| > 3\).
resi <- as.data.frame(cbind(index = 1:n, res_estud = stud_res))
ggplot(resi, aes(x = index, y = res_estud, label = index)) +
geom_point(color = "blue") +
geom_hline(yintercept = c(-3, 3), color = "red", linetype = "dashed") +
geom_text_repel(data = filter(resi, abs(res_estud) > 3)) +
labs(x = "Índice", y = "Residual Estudentizado", title = "Identificación de Outliers") +
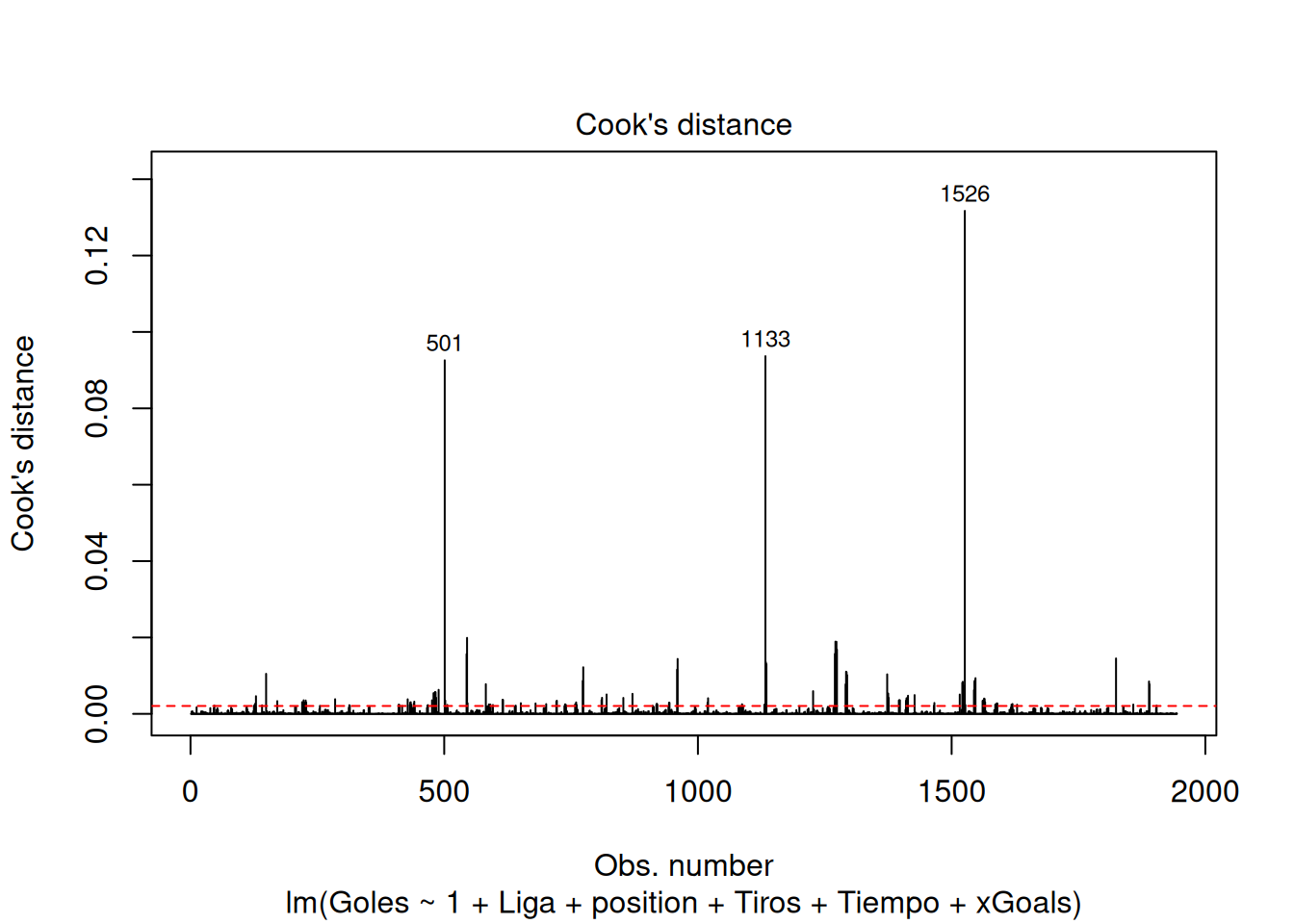
theme_minimal()17.3 5.3. Observaciones Influyentes (Distancia de Cook)
Mide el efecto de eliminar una observación. Un punto es influyente si su Distancia de Cook \(D_i > 4/(n-p-2)\).
# Gráfico de la Distancia de Cook
corte <- 4 / (n - p - 2)
plot(modelo, which = 4, cook.levels = corte)
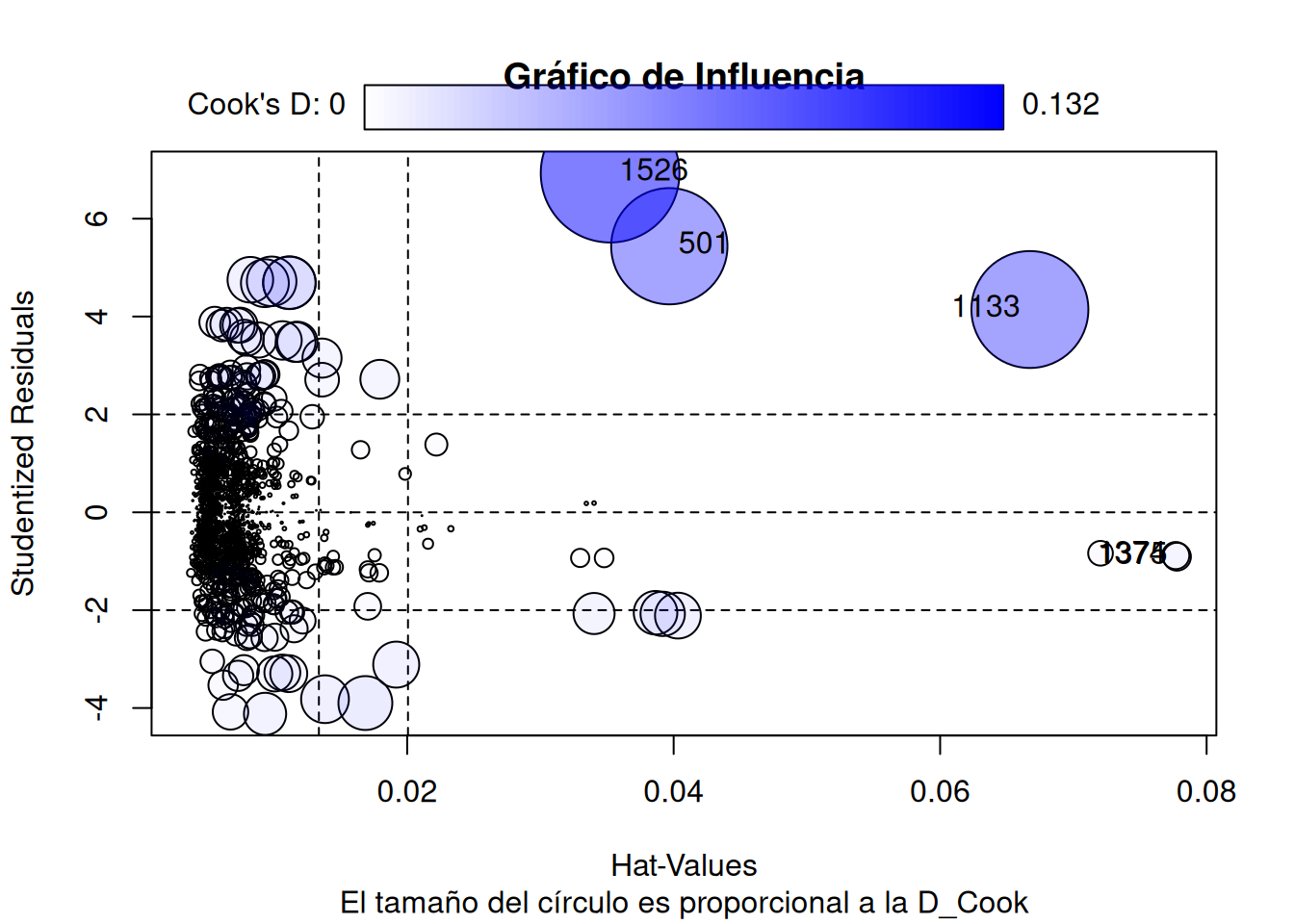
abline(h = corte, lty = 2, col = "red")# Gráfico de Influencia
influencePlot(modelo, id.method = "identify", main = "Gráfico de Influencia", sub = "El tamaño del círculo es proporcional a la D_Cook")Warning in plot.window(...): "id.method" is not a graphical parameterWarning in plot.xy(xy, type, ...): "id.method" is not a graphical parameterWarning in axis(side = side, at = at, labels = labels, ...): "id.method" is not
a graphical parameter
Warning in axis(side = side, at = at, labels = labels, ...): "id.method" is not
a graphical parameterWarning in box(...): "id.method" is not a graphical parameterWarning in title(...): "id.method" is not a graphical parameterWarning in plot.xy(xy.coords(x, y), type = type, ...): "id.method" is not a
graphical parameter StudRes Hat CookD
501 5.4370356 0.03967374 0.092573947
1133 4.1435243 0.06673625 0.093655329
1374 -0.8848279 0.07768242 0.005073005
1375 -0.9074003 0.07777160 0.005341666
1526 6.9300913 0.03523153 0.13170223917.4 5.4. Reajuste del Modelo
Se ajusta un nuevo modelo excluyendo los puntos identificados como más influyentes para evaluar su impacto en los coeficientes.
# Puntos a excluir (ejemplo basado en diagnóstico visual)
puntos_a_excluir <- c(149, 501, 544, 545, 774, 959, 960, 1133, 1134, 1135, 1270, 1271, 1272, 1273, 1274, 1292, 1293, 1294, 1373, 1526, 1824)
modelo_sin_influyentes <- update(modelo, subset = -puntos_a_excluir)
# Comparación de coeficientes
round(as.data.frame(coef(summary(modelo))), digits = 4) Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.1265 0.1128 -1.1222 0.2619
LigaLa Liga -0.0841 0.1106 -0.7599 0.4474
LigaLigue 1 -0.0073 0.1093 -0.0672 0.9464
LigaPremier League 0.0388 0.1125 0.3446 0.7305
LigaSerie A -0.0931 0.1196 -0.7782 0.4366
positionAML -0.0431 0.1154 -0.3735 0.7088
positionAMR -0.0547 0.1157 -0.4729 0.6363
positionFW -0.1084 0.1052 -1.0309 0.3027
positionFWL -0.0102 0.1313 -0.0776 0.9381
positionFWR -0.0023 0.1279 -0.0182 0.9855
Tiros 0.0277 0.0044 6.2498 0.0000
Tiempo 0.0001 0.0001 0.6242 0.5326
xGoals 0.8447 0.0220 38.3747 0.0000round(as.data.frame(coef(summary(modelo_sin_influyentes))), digits = 4) Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.0742 0.1031 -0.7194 0.4720
LigaLa Liga -0.2637 0.1018 -2.5916 0.0096
LigaLigue 1 -0.0711 0.1000 -0.7109 0.4772
LigaPremier League -0.0230 0.1028 -0.2234 0.8233
LigaSerie A -0.1028 0.1096 -0.9386 0.3481
positionAML -0.0246 0.1054 -0.2334 0.8155
positionAMR -0.0624 0.1060 -0.5885 0.5562
positionFW -0.1122 0.0965 -1.1630 0.2450
positionFWL -0.0376 0.1204 -0.3122 0.7549
positionFWR -0.0526 0.1171 -0.4496 0.6531
Tiros 0.0180 0.0042 4.2437 0.0000
Tiempo 0.0003 0.0001 3.7907 0.0002
xGoals 0.8301 0.0226 36.7296 0.0000